Week1-Specialization Introduction

이 코스의 다른점 §

수학 뿐만 아니라 Python code도 할 것임

Introduction §

실제 상황을 Matrix로 표현하게 됨. Singularity 등 Week 2 - 2 by 2, 3by 3, Rank 등 Week 3 - Vector Week 4 - Eigen vector

pre-requisite

• 간단한 수학 및 plot
  • 1 variable math
  • 2d plot
• Basic Algebra를 알고 있으면 됨

System of sentences §

Complete / Redundant / Contradictory

일상적인 문장을 이용해 각 변수가 해결 가능한 문제인지 보여줌 해결 가능한 complete를 Non-singular 같은 내용이 반복되거나 모순되는 경우는 Singular case에 해당함

graph LR
	A[System of Sentence] -- complete --> B[Non-singular]
	A -- Redundant --> C[Singular]
	A -- Contradict --> C

Complete §

• The dog(b) is black
• The cat(c) is orange
  • 위 문장은 각 변수(동물)를 계산 할 수 있음

Redundant §

• The dog is black
• The dog is black
  • 두 변수(문장)는 동일하기 때문에 문제를 풀 수 없음

Contradictory §

• The dog is black
• The dog is white
  • 두 문장은 모순됨

System of equations §

Complete / Redundant / Contradict

앞서 문장을 통해 문제를 해결하는 방법을 보여줌.여기에서는 위 문장을 수학식으로 정의하고 해결 방법을 보여줌

Complete §

• $a+b=10$
• $a+2b=12$
  • $a=8,b=2$
  • Non-singular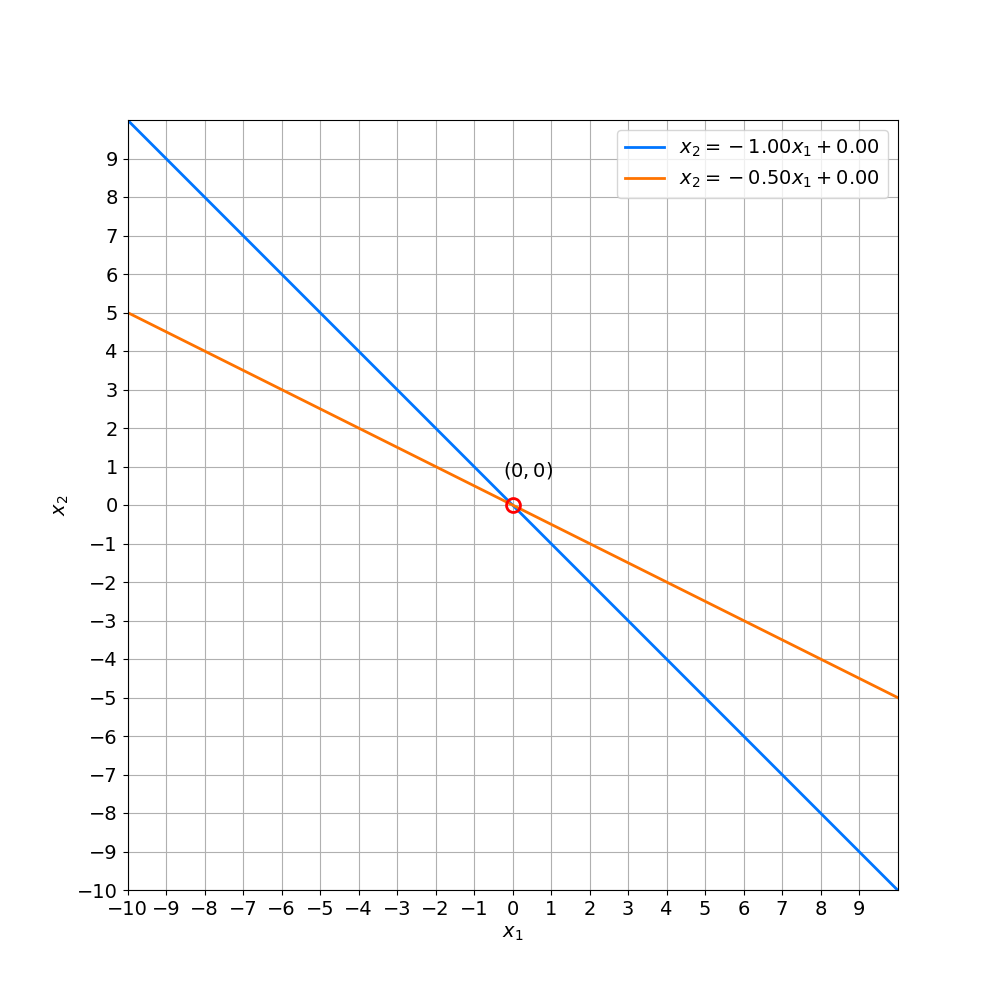

Redundant §

• $a+b=10$
• $2a+2b=20$
  • 무한히 많은 해답이 존재함
  • Singular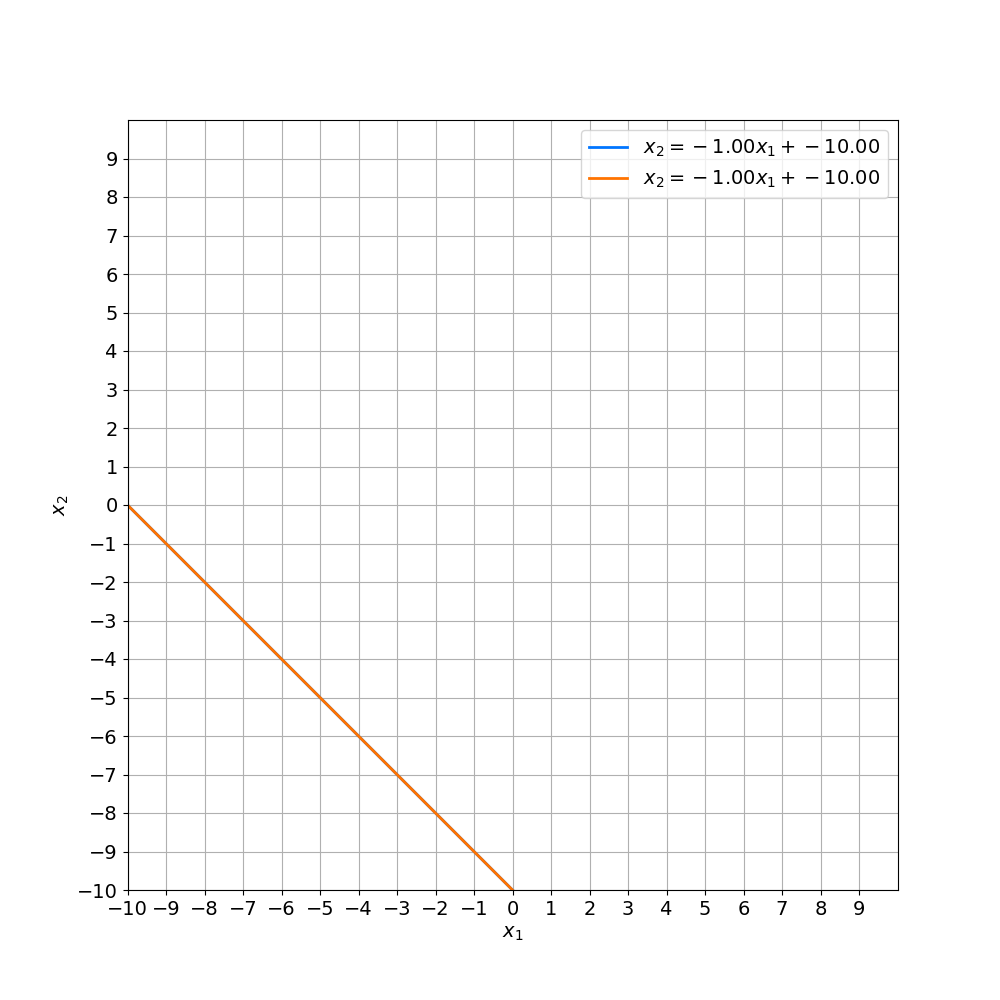

Contradictory §

• $a+b=10$
• $2a+2b=24$
  • 모순되기 때문에 답이 존재하지 않음
  • Singular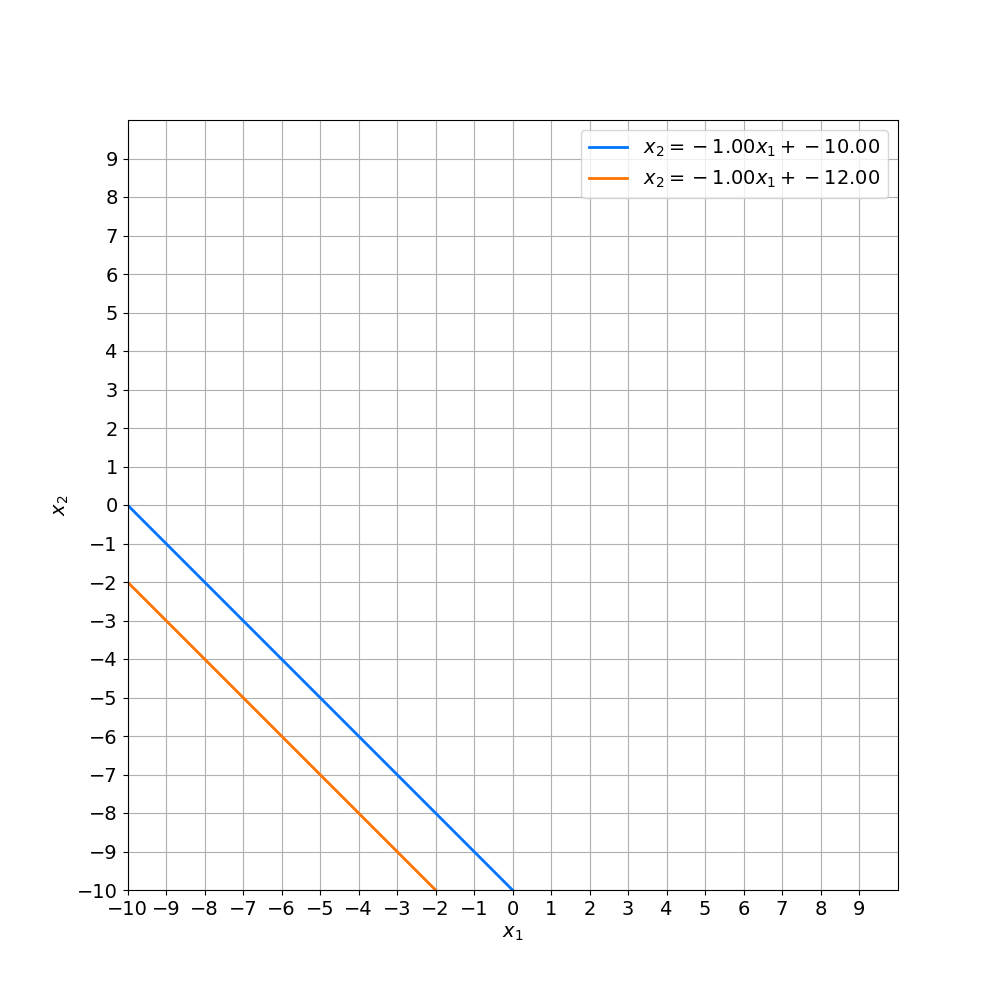

Linear Equation §

선으로 표현 가능 한 식(2D)

선형 식은 좌표에 선으로 표현 가능함

System of equation as Line §

• 변수가 두개인 matrix는 2d space의 Line으로 표현 가능 함

Geometrical meaning of Singularity §

• Linear equatuon이 Singular
  • Inifite or No solution
    • 즉, 두 선이 평행하거나 겹쳐있는 경우를 뜻함
• Non-Singular
  • 두 선이 평행하지 않음을 뜻함

Linearly dependant rows and Determinant §

2*2 matrix와 determinant

2*2matrix의 determinant를 이용해 각 row가 linear dependent 한지 알 수 있음. 다시말해 linearly dependent 하면 해답이 무한하거나, 없음(singular)

• Linearly dependant row는 2*2 matrix에서 한 row가 다른 row의 k배가 된다는 것을 뜻함
• 해당 속성을 이용하면 $ad-bc=0$ 인 경우 해답을 찾을 수 없음을 알게됨
• $\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\text{in linear dependeant rows, }c=ka,d=kb$
• $k=a/c=d/b->ad=bc->ad-bc=0$

Study question

1. Determinant는 n 정사각 행렬에 대해서 구할 수 있는 값인가?
2. 그렇다면 n 정사각 행렬의 linear dependancy를 판별하기는 쉬운일
3. 아니라면 그 외의 행렬은 어떻게 처리 되는가?
   1. 가로로 긴 행렬은 생각해보면 이미 문제를 풀기위한 충분한 정보가 부족함
      1. $\left[\begin{array}{ccc}a& b& c\\ d& e& f\end{array}\right]$
   2. 세로로 긴 행렬의 경우 중복되는 정보 또는 모순 될 수 있음을 뜻한다 볼 수 있음
      1. $\left[\begin{array}{cc}a& b\\ c& d\\ e& f\end{array}\right]$

3by 3 matrix §

Singular하면 답을 구할 수 없다

한 row가 다른 row의 linear combination인 경우 singular함. Singular한 경우 해답은 무한히 많거나, 존재하지 않음 singularity를 계산할때는 constant(우변의 값)은 중요하지 않음

• 예)
• $\left[\begin{array}{ccc}1& 1& 1\\ 1& 2& 1\\ 1& 1& 2\end{array}\right]\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 2\\ 1& 1& 3\end{array}\right]\left[\begin{array}{ccc}1& 1& 1\\ 2& 2& 2\\ 3& 3& 3\end{array}\right]$
• 첫번째 식은 답이 있고 나머지는 해답이 존재하지 않음

Determinant of 3 by 3 matrix §

• 3 by 3 메트릭스의 determinant는 다음과 같이 구할 수 있음
• $\left[\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right]->aei+bfg+cdh-ceg-bdi-ahf$

study question

• 위 메트리스의 디터미넌트는 어떻게 유도되는가?
  • hint: 각 row 중 어느 한 관계라도 Linear dependent하다 -> 각 row별 Determinant를 곱하면 0이 된다

Week1 - Numpy part §

#linearalgebra#deeplearningai#numpy