https://codebastardarch.pages.dev/ 의 작업을 보고 인상받아 직접 코드로 한번 구현해 봤다. 아쉬운점은 이게 제대로 짜여진 코드가 맞는지 나도 알 수 없는 부분들이 있어서 일단은 그냥 써본다
1 Q-learning recap
옵시디언을 쓰면 내용들을 링크하는게 가능하지만 그래도 정리차원에서 어느정도는 재반복으로 관련내용을 쓰기로 했다. Q-learning은 off-policy, TD based, Value based method 이며, 계산 과정에서 내부적으로 Q-table을 사용한다. Q-table에는 각 state,action pair의 value(action value)가 저장된다. 이를 이용해 Q-function을 학습시키면 된다.

가령 원래 렉쳐의 경우를 가져와 다시 설명하면 이렇다. 위 그림에서 쥐가 있을 수 있는 위치(타일)는 6개다. 그렇다는 것은 state는 6개로 정의 할 수 있다. 각 위치에서 취할 수 있는 행동은 위,아래,좌,우 4가지가 된다. 이 상태를 그림으로 표현해보면 아래와 같아진다.
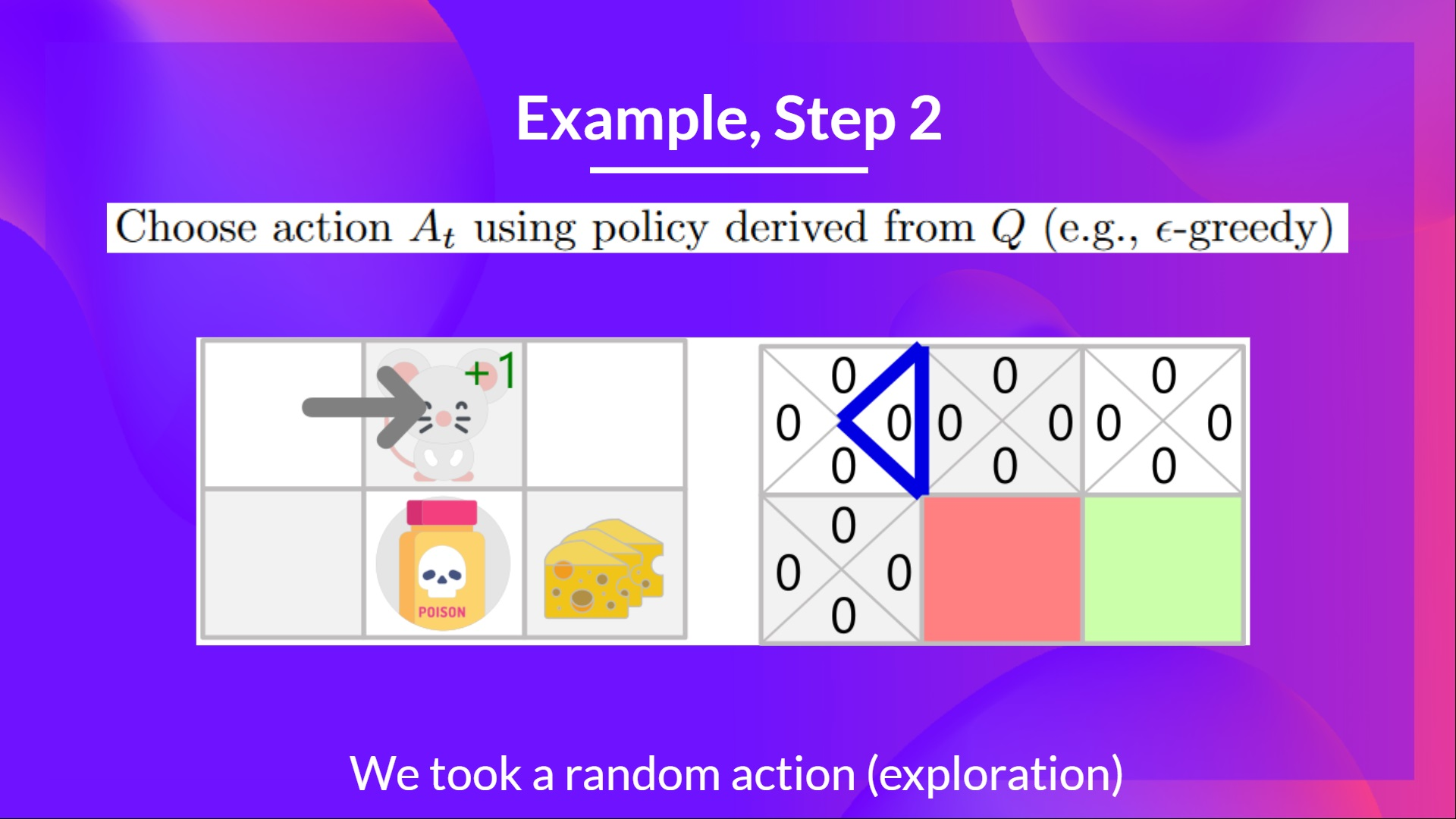
각 위치에서 움직일 수 있는 위치가 4가지기 때문에 위처럼 4개의 타일로 쪼개서 그림으로 표현한다. 그리고 빨간색과 초록색은 terminate state를 뜻한다. 게임으로 치면 져서 게임을 종료하던, 엔딩을 봐서 종료하던 그런 상황을 의미한다. 위 그림을 테이블로 만들면 Q-table이 된다. 다행히도 2차원으로 표현 가능하다. 위 state를 언롤하듯 x축으로 만들면 아래 테이블이 된다.
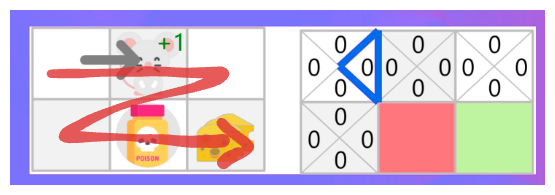

코딩 스타일에 따라 위 테이블에 접근하기 위한 row를 tuple 형태로 하거나(왜냐면 원래는 x,y위치로 볼 수도 있으니까) 0~#of state-1로 하기도 한다. 전자나 후자나 나름의 고충은 존재한다. 내가 본 예제들은 후자를 주로 따르니 후자를 기준으로 했다.
2 Pseudo code
여기서는 두개의 Pseudo code를 언급할 필요가 있다. 하나는 수학적으로 정의된 Q-learning이다. 이게 근간이 되어야 뭘 할 수 있다. 그리고 이 코드르 직접 쓰기위해 내가 어떤 흐름으로 했는지 보여주는 Pseudocode 두가지를 소개한다.
2.1 이론 수학
이론적 설명은 8 A Q-Learning example에 해놨으니 여기에는 그림만 놓는다.

2.2 내 코드
# 넘파이, 랜덤, tqdm 라이브러리를 로드함
# 글로벌 변수 설정
## state의 수
## action의 수
## Dead state
## winning state
# reward table을 정의 함
# q-table을 정의 함
# randomAction 기능을 정의함
## 액션은 랜덤으로 하나 선택하게 됨
## 그러나 현재 상태를 기준으로 액션을 취했을때, 테이블 바깥으로 벗어나면 다시 새로운 랜덤을 정의해야함
## 랜덤 액션을 리턴함
# greedyAction 정의
## Q-table에서 해당 state중 가장 높은 action value의 action return
# epsilongreedy
## epsilon factor를 정의함
## Epsilon factor와 eps를 비교해 action 선택
# step
## 해당 state에서 action을 되는지 안되는지를 알려줌. 가령 모서리 부분에서는 바깥으로 나가면 안되는 경우들을 방지해주는 여할
## 0,1,2,3 -> up,right,down,left(시계방향)으로 정의함
## action이 0이고 현재 state에서 위로 올라갈때 index가 0보다 크거나 같으면 -> update state
## action이 1이고 오른쪽이 table의 바깥이 아니라면 -> update
## action이 2이고 업데이트 위치가 max state보다 작으면 -> update
## action이 3이고 업데이트 위치가 왼쪽 바깥이 아니면 -> update
## 모두 해당 안되면 제자리에
# 학습
## 최대 에피소드
## 디케이 레이트(입실론이 줄어드는 비율)
## 러닝레이트
## 감마(할인율)
## 입실론
## 최대 스탭(한 에피소드에서 최대로 탐색 가능한 스탭
## 종료 위치
## 각 에피소드에서
## - 임의 위치에서 시작
## - 해당 위치부터 최대 스탭까지
## -- 만약 현재 위치가 종료위치면 종료
## -- 액션은 입실론 그리디
## -- 새 스테이트는 step function을 토앻
## -- 리워드는 리워드 테이블에 새 스테이트를 넣어서
## -- TD update
## -- 현재 스테이트 = 새 스테이트
## - 입실론 디케잉
## Q-table 리턴허깅페이스에서 제공하는 예제의 Q-table 결과물과 비교했을 때 위 방식이 맞는거 같다. 아주 간단한 수학이지만 그래도 좀 꼼꼼함이 필요한 것은 step 부분이었는데 관련한 그림으로 설명해보면 아래와 같다.
 가령 내가 3*5 = 15 만큼의 state를 정의했다고 가정해보자. 그러면 이를 위에서 언급했듯 unroll하면 위 그림처럼 0,1,...,14의 형태가 된다. 이 상태에서 어떤 경우에 table 바깥으로 벗어나게 되는지 정의하는 것이 핵심이다. 위 그림 중 4위치를 중심으로 문제를 설명해보면 다음과 같다. unroll된 list를 보고 판단했을때, 4의 위치에서 오른쪽으로 이동 가능해 보인다. 그러나 2차원 테이블로 보면 그게 불가능 하다는 것을 볼 수 있다
가령 내가 3*5 = 15 만큼의 state를 정의했다고 가정해보자. 그러면 이를 위에서 언급했듯 unroll하면 위 그림처럼 0,1,...,14의 형태가 된다. 이 상태에서 어떤 경우에 table 바깥으로 벗어나게 되는지 정의하는 것이 핵심이다. 위 그림 중 4위치를 중심으로 문제를 설명해보면 다음과 같다. unroll된 list를 보고 판단했을때, 4의 위치에서 오른쪽으로 이동 가능해 보인다. 그러나 2차원 테이블로 보면 그게 불가능 하다는 것을 볼 수 있다

따라서 unroll된 테이블을 2차원으로 해석해서 오른쪽으로 이동가능한지 불가능한지 판별하는 로직이 필요하다. 이를 위해서는 table의 폭을 이용해 각 값의 나머지(remainder)를 구함으로서 해결할 수 있다. 가령 위 예시에서 테이블의 폭은 5가 되며 각 나머지를 구하면 다음과 같다.
 이 방법을 통해 어느 한 state에서 왼쪽 오른쪽으로 이동 가능한지 판별 할 수 있다. 지금 생각해보니 이 방식을 이용해 row를 판별하는 방법도 가능하지만 굳이 이렇게 까지 안해도 up,down은 판별이 가능하다
이 방법을 통해 어느 한 state에서 왼쪽 오른쪽으로 이동 가능한지 판별 할 수 있다. 지금 생각해보니 이 방식을 이용해 row를 판별하는 방법도 가능하지만 굳이 이렇게 까지 안해도 up,down은 판별이 가능하다
3 최종 코드
import numpy as np
import random
from tqdm import tqdm
STATE_ROWS = 4
STATE_COLS = 4
ACTIONS = 4
DEAD_STATE = 7
WIN_STATE = 4
REWARD_TABLE = np.zeros(STATE_COLS*STATE_ROWS)
REWARD_TABLE[3] = 1
REWARD_TABLE[WIN_STATE] = 10
REWARD_TABLE[DEAD_STATE] = -10
REWARD_TABLE[9] = 1
Q_TABLE = np.zeros((STATE_COLS*STATE_ROWS,ACTIONS))
def randomAction(state):
action = random.randint(0,ACTIONS-1)
if step(state,action) == state:
action = randomAction(state)
return action
def greedyAction(state):
action = np.argmax(Q_TABLE[state][:])
return action
def epsGreedy(state:int,eps:int)->int:
epsFactor = random.uniform(0,1)
if epsFactor <= eps:
action = randomAction(state)
else:
action = greedyAction(state)
return action
# actino 0,1,2,3 -> up,right,down,left
def step(state:int,action:int)-> int:
if action == 0:
if state-STATE_COLS >= 0:
return state - STATE_COLS
if action == 1:
if state%STATE_COLS != STATE_COLS-1:
return state + 1
if action == 2:
if state + STATE_COLS < STATE_COLS*STATE_ROWS:
return state + STATE_COLS
if action == 3:
if state%STATE_COLS != 0:
return state - 1
return state
print(step(3,3))
def train():
max_episodes = 10000
decay_rate = 0.999
learning_rate = 0.7
gamma = 0.90
eps = 1.0
max_step = 15
terminal_state = {WIN_STATE,DEAD_STATE}
for i in tqdm(range(max_episodes)):
state = random.randint(0,STATE_ROWS*STATE_COLS-1)
for j in range(max_step):
if state in terminal_state:
break
action = epsGreedy(state,eps)
new_state = step(state,action)
reward = REWARD_TABLE[new_state]
Q_TABLE[state][action] = Q_TABLE[state][action] +\
learning_rate*(reward + gamma *\
np.max(Q_TABLE[new_state])
- Q_TABLE[state][action])
state = new_state
eps *= decay_rate
return Q_TABLE3.1 return 결과물
reward table
[[ 0. 0. 0. 1.]
[ 10. 0. 0. -10.]
[ 0. 1. 0. 0.]
[ 0. 0. 0. 0.]]
Q-table
[[ 0. 8.1 10. 0. ]
[ 0. 7.29 9. 9. ]
[ 0. 7.561 8.1 8.1 ]
[ 0. 0. -10. 7.29 ]
[ 0. 0. 0. 0. ]
[ 8.1 8.1 9.1 10. ]
[ 7.29 -10. 8.19 9. ]
[ 0. 0. 0. 0. ]
[ 10. 9.1 8.1 0. ]
[ 9. 8.19 8.19 9. ]
[ 8.1 7.371 7.371 9.1 ]
[-10. 0. 6.6339 8.19 ]
[ 9. 8.19 0. 0. ]
[ 9.1 7.371 0. 8.1 ]
[ 8.19 6.6339 0. 8.19 ]
[ 7.371 0. 0. 7.371 ]]위 스크립트를 돌리면 아마도 다음과 같은 결과물을 얻을 수 있을 것이다. 결과물을 해석해보면 Q-learning이 제대로 된 것 같다. 몇가지를 sample로 보면 아래와 같다
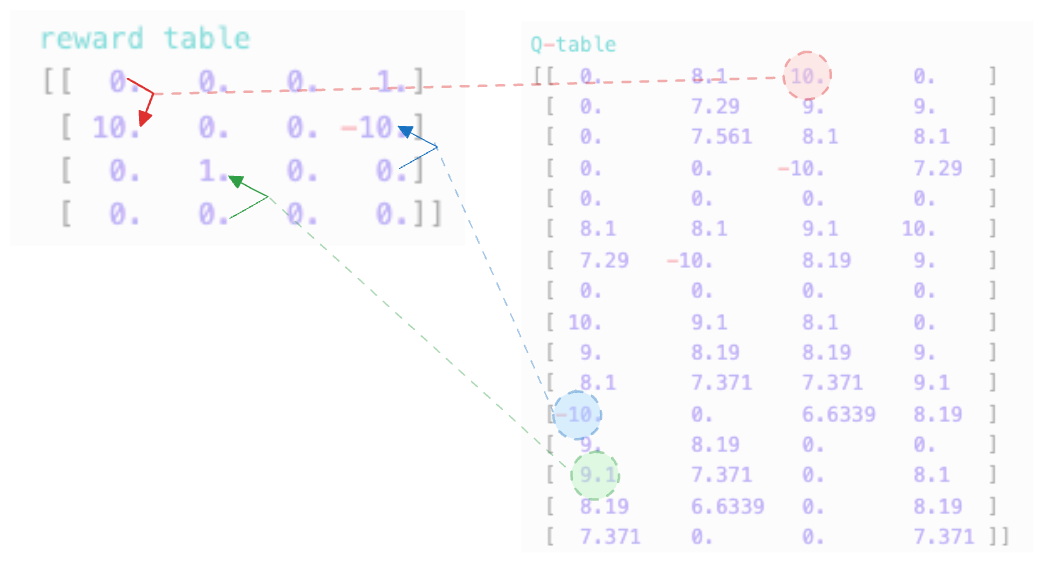 위 빨간색 에서는 아래로갈때 (action=3) 가장 큰 보상을 받을 수 있다. 바로 10의 reward를 받을 수 있기 때문이다. 다른 자잘한 reward(1)을 합친 후 가는 방향도 고려해 볼 수 있지만, 할인율을 적용해 봤을때, 바로 10의 reward를 받고 끝내는 것이 가장 큰 보상을 받는 바법이다.
위 빨간색 에서는 아래로갈때 (action=3) 가장 큰 보상을 받을 수 있다. 바로 10의 reward를 받을 수 있기 때문이다. 다른 자잘한 reward(1)을 합친 후 가는 방향도 고려해 볼 수 있지만, 할인율을 적용해 봤을때, 바로 10의 reward를 받고 끝내는 것이 가장 큰 보상을 받는 바법이다.
파란색의 경우 위로 이동하면 -10을 받고 끝나게 되는 부분이 잘 포현되어 있다.
초록색은 위로 갔을때 9.1의 보상을 받게 되는 것을 표시하고 있다. 그 이유는 바로 받는 보상 1과 state중 가장 큰 보상을 받는 () 값에 할인율을 곱한 8.1이기 때문이다.
4 후기
내용이 슬슬 어려워지는 점도 있지만 그래도 전체적인 내용이 잘 정리되어 있어서 풀기 편했다. 다시한번 라이브 코딩을 해준 https://codebastardarch.pages.dev/ 님께 감사를 표하며 글을 마친다.